Our Microsiphon
A Failsafe Microsiphon
The write up is based on data obtained from our own experience. Your result may differ from ours. Use at your own risk. Also, if you notice lack of scientific citations, please note it started as a fun craft project done quickly for a friend who wanted an aquaponics kit for her coffee table.

Justponics Microsiphon
This microsiphon is optimized for 1 to 10 gallon tank with an operating flow rate of 10 to 40 gallons per hour
Research beginnings
In the beginning, I researched the math behind hydrodynamics wave propagation but came to learn that the problem was a complicated one, and had not yet been rigorously solved analytically. Instead, a series of assumptions and simplifications were often used in practice. The fluid wave propagation was a three-dimensional problem, but it was simplified from three-dimensional to a one-dimensional problem by using Webster’s horn equation. I got useful information about the behavior with this type of approach. A large number of cases were solved this way with high satisfaction. I got a really lucky break when I made the further assumption that water is a type of high viscous air. It is indeed a lucky break for me because the math on aerodynamics was abundantly available.
Three inventions to help start the siphon
Bell Siphon Veloster
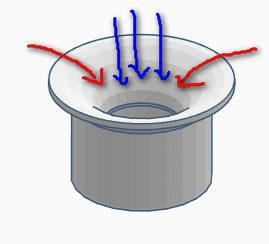
Water movement in Veloster
The red arrows indicate slow water movement and the blue arrow indicates fast water movement
Th bell siphon Veloster is a specially shaped hydrodynamics device designed to facilitate failsafe starting of siphon by passing a large volume of water into a narrow riser pipe. Without the Veloster, water will attempt to drain simultaneously creating a traffic jam. The science here is a reversal of impedance resonance. The impedance resonance is why a trumpet can carry a tiny lip vibration at the trumpet mouthpiece over a great distance. The boundary layer development was critical in achieving strong siphon because the high viscosity of water produces high shear stresses, and distorts the inner non-viscous flow. The device achieves compressed entry of water by transitioning slow water to fast water flow. Entering water is smoothed out, and the flow fills the entire pipe area.
The S-Strap

S-Strap water column
S-Strap creates a back pressure for siphon to start
S-trap is a curved hydrodynamics device designed to facilitate minimizing siphon as long as possible so that maximum siphon is achieved through a sudden jump in the water velocity. It operates fundamentally different from the 90-degree elbow. The scientific method here is Stick and Slip phenomenon. Stick-slip can be described as surfaces alternating between sticking to each other and sliding over each other, with a corresponding change in the force of friction. If an applied force is large enough to overcome the static friction, then the reduction of the friction to the kinetic friction can cause a sudden jump in the velocity of the movement. You can see the water column inside a bell rise in stick and slip motion fashion.
The snorkel
Side view of snorkel
A snorkel is a special internal snorkel piping designed to facilitate failsafe stopping of siphon. It passes a large volume of air into a narrow riser pipe without interruption. The science here is Stoke’s Law. A bubble starts out as compressed gas equal to the surrounding fluid pressure when it was first formed. As a bubble rises it loses initial acceleration and reaches terminal velocity while increasing in size causing more drag. Which means a bubble at terminal velocity does not have enough kinetic energy to effectively stop the siphon. We want a fast bubble to reach the top quickly so the siphon can stop quickly. The change in the velocity and direction of movement are kept as gradual as possible to attain the highest economy by applying the principle of laminar flow. The specific calculation of the Reynolds number is satisfied by manipulating the geometry of the flow system and flow pattern. The bubble is given the straightest path of least resistance by a snorkel.
LPH Formula
The flow rate of a siphon is a function between the diameter of standpipe and S-trap. The equation is as described by Bradbury (1910) gives the average flow rate as
Q = K × A × (2 × G × H)1/2
Water inflow is achieved by a 300LPH (80GPH) submerged pump which can be purchased for ~$10.
Because the inflow rate is depended on the capacity of the pump and the pumping height, we determined 300LPH (80GPH) rated pump was achieving 150LPH (40GPH) actual pumping rate when the pumping height was at 280 mm. 280 mm was calculated by assuming stacking two 140 mm height bins. We kept the pump at the lowest part of the lower bin and water outlet hose at the highest part of the upper bin.

Salma 1 gallon plastic bin found at ikea.com
Width: 280 mm , Depth: 190 mm , Height: 140 mm , Volume: 3.8 liter , Material: Polypropylene (C3H6)n
We designed the Edu Kit for indoor use only so we believe beneficial physical properties of PP such as good chemical resistance with good elasticity and good fatigue resistance outweigh PP’s susceptibility to UV degradation. The replacement bin can be purchased economically from Ikea.com. In any case, please do not use the Edu Kit outdoors or under direct sunlight.
Since it would have been more optimum if the pump was cut off during the discharge, we considered a float valve switch design to cut off the pump when the siphon started. This design was put on hold as a float valve switch would have taken up valuable grow bed space.
Optimum Pump Performance
In our calculation, 150LPH (40GPH) was most reasonable for 3.8 liters (1 Gallon) IKEA samala bin at 280 mm pumping height. The siphon started surely and ended satisfyingly without fail and worry, every single time. We called this a “one-siphon-to-rule-them-all” stage.
As we have calculated and demonstrated, the success of siphon depends largely on correct calibration based on the tank’s volume (width x depth x height, 3.8 liters in our case), the surface area (width x depth), water flow rate (water inflow – water outflow). There was a strong linear relationship between the water flow rate and trigger/break action with a coefficient of determination of 0.99.
One more important dimension of considerations was how fast water could rise. This is a derivative of the net water flow rate and bin dimension. For a given net water flow rate and a bin volume, a narrow bin would achieve faster water rise than a wide bin. A faster water rise from a narrow bin will aid in the starting of the siphon. A slower water rise from a wide bin may not be able to start the siphon. A calculation based on actual water inflow rate alone would only be correct if we assume the grow bed is always used empty. The water rise rate depended on how densely medium (sand, pebble, hydroton, etc) was packed in addition to actual water inflow rate which depended on actual pump rate and pump height and in addition to how wide or narrow the bin was shaped.
Conclusion
To quote one of our fans’ comment posting, “It just works”
